10月頭より再挑戦し始めたあまりのある割り算。九九で解ける割り算はスラスラ答えが出るのに、あまりがあるとやはりまだまだ手こずっています。
再開当初は、順番に並んでいる割り算の問題に、あまりを単に増やしていくような感じで考え、慣れていきました。
7 ÷ 3 = 2…1 ← 1増えただけだから解ける
8 ÷ 3 = 2…2 ← あまりが1ずつ増えるから解ける
9÷ 3 = 3 ← 九九で解ける
しかし、進めるに連れて問題の並びが穴抜けになってきて、その方法では上手くいかなくなり正攻法で考える必要が出てきました。
7 ÷ 3 = 2…1 ← 1増えただけだから解ける
8 ÷ 3 = 2…2 ← あまりが1ずつ増えるから解ける
10 ÷ 3 = ← ???
こういう場合は、3の九九を思い出して、3×3=9、3×4=12と割られる数10を超える答えを探して、超えたら一つ前の3×3の3を商とする、そして10-9=1があまりとなる、と考えます。
前回の記事でも書きましたが、あまりの出し方については、引き算をするというのが分かりにくいらしく10-9=1と引き算で考えるのではなく、9+□=10となる□を考えるようにすると直ぐにあまりが出せるようになりました。
しかし、今度は穴抜けになっている場合の商の出し方に戸惑っている様子。どうも一つ前というのがピンと来ないようで作業的になり、こんがらがっていました。
そこで、その計算過程は何を表しているのかを図示化して説明しました。
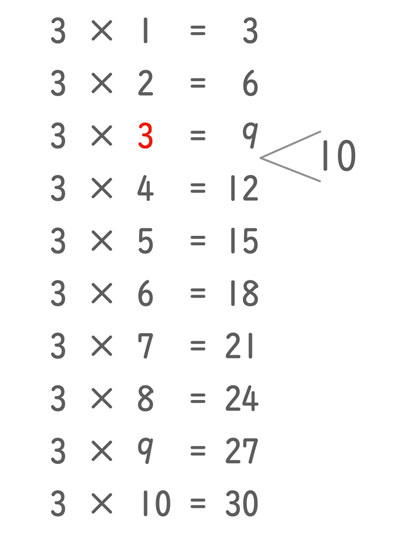
- 10 ÷ 3 =
10は3のかけ算の答えの列(3, 6, 9, 12, 15…)の中でどこの間に入るか、考える。 -
10 ÷ 3 = 3 …
3×3 = 9 と 3×4 = 12 の間にある。かける数は3より大きく4より小さいとわかる。なので商は3。 - 10 ÷ 3 = 3 …1
3×3 = 9 を10 にするには、1 必要。なのであまりは1。
こんな感じに、なぜ九九で超える場合、前のかけ算のかける数が商になるのかを説明したところ、多少理解が深まったのか、穴抜けの問題でも商を見つけられるようになってきました。
取り組み中の「くもんの小学ドリル 3年わり算」では「あまりのあるわり算」が(14)まであり、現在(5)までを演習しています。単純に順番に並べているようで、少しずつ穴が空いてきたり順番が不規則になっていき、最終的に自力で考えるように促しているあたりが、市販のドリルとはいえ問題の出し方に公文らしさが出ているなぁと感じます。
たろすけ本人もいよいよ自力で解けるようになってきて自信が出てきたようです。焦らず、着実に進めていきます!

これまでの「あまりのあるわり算」に関する記事




コメント